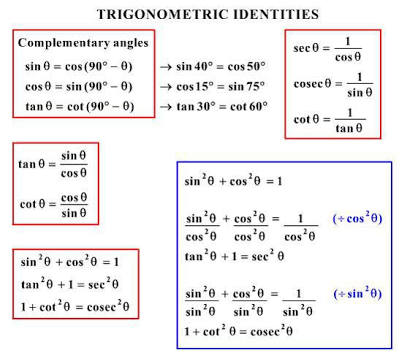
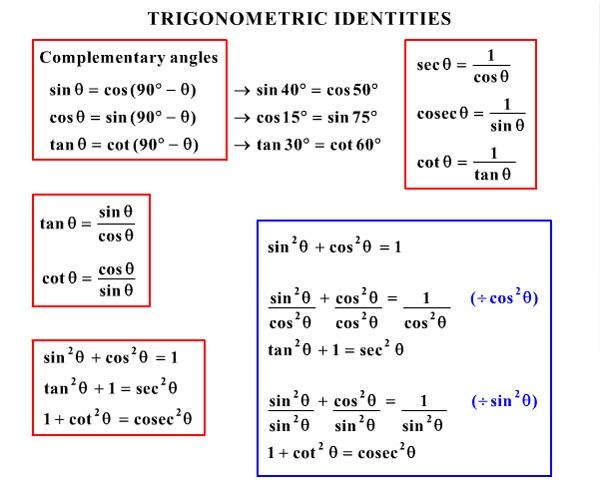
Trigonometric Formulas Here, you can learn all type of trigonometric formulas TRIGONOMETRIC FORMULAS sec² 2 θ tan 2 θ = 1 sec 2 θ = 1 tan 2 θ tan 2 θ = sec 2 θ 1 cosec 2 θ cot 2 θ = 1 cosec 2 θ = 1 cot 2 θ cot 2 θ = cosec 2Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more0911 · Defining Tangent, Cotangent, Secant and Cosecant from Sine and Cosine tan θ = sin θ cos θ cot

Prove That Cot Theta Tan Theta 2 Cot 2theta Youtube
Tan^2 theta cot^2 theta formula
Tan^2 theta cot^2 theta formula- · tan theta – cot theta/sin theta cos theta = tan^2 theta – cot^2 theta More Articles If the roots of the equation (ab)x^2 (bc)x(ca) =0 then prove that bc=2a cosec theta – cot theta whole square = 1cos theta/1cos theta Class 10 Ex 84 Q 5 i Related Categories Education Post navigation(tan θ cot θ) = 5 Squaring on both sides (tan θ cot θ)² = (5)² tan² θ cot² θ 2 × tan θ × cot θ = 25 tan² θ cot² θ 2 × tan θ × 1/tan θ = 25 tan² θ cot² θ



How Does The Trigonometric Identity 1 Cot 2 Theta Csc 2 Theta Derive From The Identity Sin 2 Theta Cos 2 Theta 1 Mathematics Stack Exchange
Now, learn how to expand trigonometric functions with multiple angles The following multiple angle identities are used as formulae in mathematics Double angle formulas Learn how to expand double angle trigonometric functions in terms of trigonometric functions $(1)\,\,\,\,$ $\sin{2\theta}$ $\,=\,$ $2\sin{\theta}\cos{\theta}$If tan ^2theta = 2tan ^2ϕ 1, then cos 2theta sin ^2ϕ equalsSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more
The second shows how we can express cos θ in terms of sin θ Note sin 2 θ "sine squared theta" means (sin θ) 2 Problem 3 A 345 triangle is rightangled a) Why?Sec 2 θ = 1 tan 2 θ for 0° ≤ θ < 90° Cosec 2 θ = 1 cot 2 θ for 0° ≤ θ ≤ 90° Class 10 Maths Formulas For Algebra & Quadratic Equations To know the algebra formulas for Class 10, first, you need to get familiar with Quadratic EquationsFree math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor
To see the answer, pass your mouse over the colored area To cover the answer again, click "Refresh" ("Reload")Prove the Following Identities (1 Tan^2 θ)/(Cot^2 θ 1) = Tan^2 θ CISCE ICSE Class 10 Question Papers 301 Textbook Solutions Important Solutions 2864 Question Bank Solutions Concept Notes & Videos 233 Time Tables 15 SyllabusProve each of the following identities `(tan theta)/((1 tan^(2) theta)^(2)) (cot theta)/((1 cot^(2) theta)^(2)) = sin theta cos theta `



The Reciprocal Trigonometric Functions Problem 3 Trigonometry Video By Brightstorm


Relating Trigonometric Functions Trigonometry Socratic
· So, $$\tan^2(3\theta) = \cot^2\alpha = \tan^2(\pi/2\pm\alpha)$$ $$\tan^2(3\theta)=\tan^2(n\pi\pi/2\pm\alpha)$$ As $\cot(\pi/2\pm\alpha) = \mp\tan\alpha\implies \cot^2(\pi/2\pm\alpha) = \tan^2\alpha$ and $\tan$ has periodicity of $n\pi$ $$3\theta = n\pi \pi/2\pm \alpha$$In each problem verify the given trigonometric identity \quad \frac{\sec ^{2} \theta}{1\cot ^{2} \theta}=\tan ^{2} \theta But from equation number one, we know that it's value is equal toe one So this is equal toe dance square teeter into one which is equal to 10 Score teeterThe first shows how we can express sin θ in terms of cos θ;



Trouble Applying The Tan Double Angle Formula For 5 Tan 2 Theta 4 Cot Theta Mathematics Stack Exchange
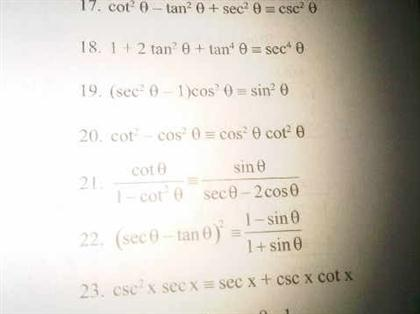


Solved Cot 2 Theta Tan 2 Theta Sec 2 Theta Csc2 Theta Chegg Com
· Calculate general solution of the equation tan 2 θ (2 – √6) tan θ – √2 = 0 7 In a triangle, the length of the two larger sides are 12 cm and 7 cm, respectivelyCos^2 theta / (cot^2 theta cos^2 theta) = 3 Answer by jsmallt9(3758) Algebracom's formula software for some reason does not "do" theta So I will be using just "t" instead of theta Algebracom's formula software does not handle powers of functions well You may see some multiplication symbols, "*", between the function and the argumentsCos (A B) = Cos A cos B – Sin A sin B Let's equate B to A, ie A = B And then, the first of these formulae becomes Cos (t t) = Cos t cos t – Sin t sin t so that Cos 2t = Cos2t – Sin2t And this is how we get second doubleangle formula, which is so
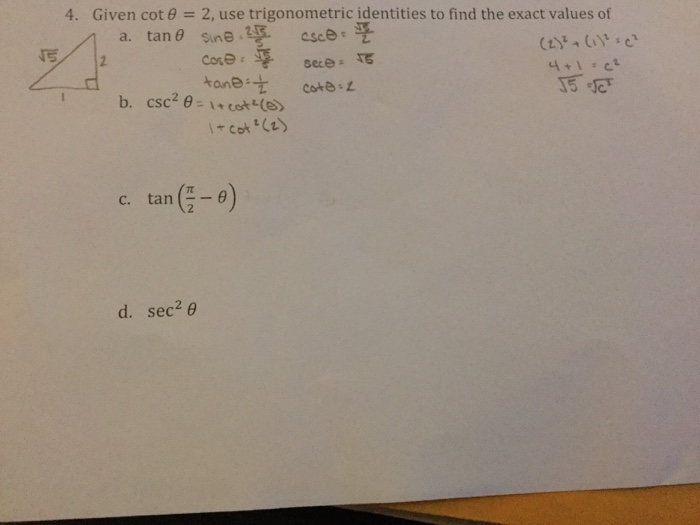


Solved Given Cot Theta 2 Use Trigonometric Identities Chegg Com



Prove The Following Trigonometric Identity Cos 2 90 Theta Cos 2theta Sec 2 90 Theta Cot 2theta Mathematics Topperlearning Com Blqep344
· The expression is 1 tan2θ = 1 sin2θ cos2θ = cos2θ sin2θ cos2θ = 1 cos2θ = sec2θ Answer link Harish Chandra Rajpoot Jul 16, 18 1 tan2θ = sec2θDividing this identity by either sin 2 θ or cos 2 θ yields the other two Pythagorean identities 1 cot 2 θ = csc 2 θ and tan 2 θ 1 = sec 2 θ {\displaystyle 1\cot ^{2}\theta =\csc ^{2}\theta \quad {\text{and}}\quad \tan ^{2}\theta 1=\sec ^{2}\theta } · tan(θ 2) cot( θ 2) = sin(θ 2) cos(θ 2) cos(θ 2) sin(θ 2) = sin2(θ 2) cos2(θ 2) sin(θ 2)cos(θ 2) = 1 sin(θ 2)cos(θ 2) = 2 2sin(θ 2)cos(θ 2) = 2 sinθ



Prove That Tan 2 Theta 1 Tan 2 Theta Cot 2 Theta 1



Trigonometric Identities Simplify Expressions Video Lessons Examples And Solutions
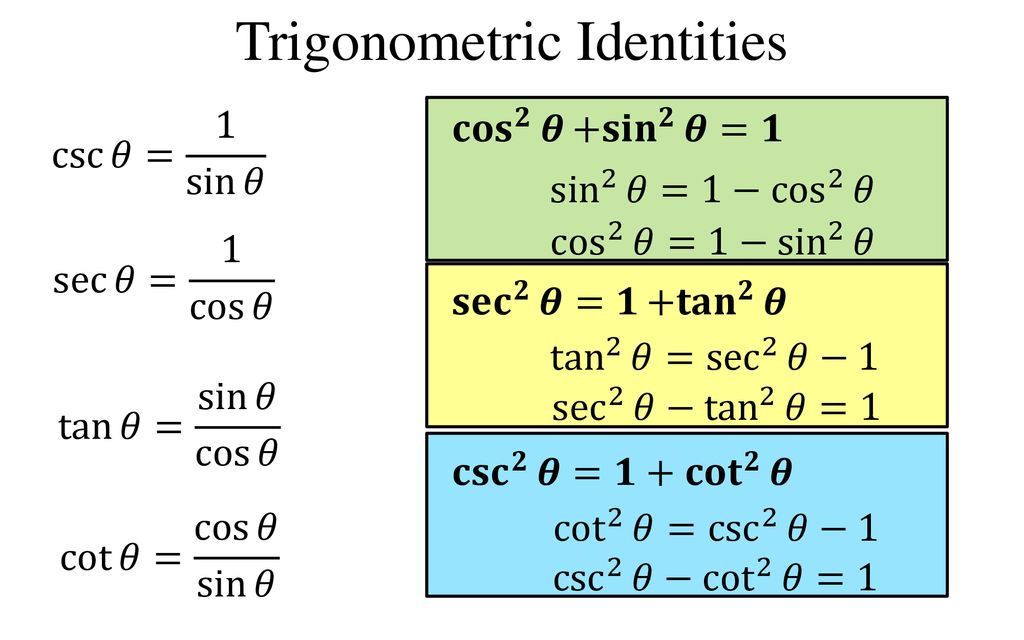
Sin 2 θ cos 2 θ = 1;0506 · The given formula is $$ 0 = \cos{2\theta} \sin{2\theta}\tan{\phi} $$ And it is simplified to $$ \theta = \frac{1}{2}\tan^{1}{\left(\frac{1}{\tan{\phi}}\right)} $$ I don't really see how you can get there from the given foruma I've tried moving things around in the equation but it never gives me the proper result · 1tan2⠡θ=sec2⠡θand1cot2⠡θ=csc2⠡θ{displaystyle 1tan ^{2}theta =sec ^{2}theta quad {text{and}}quad 1cot ^{2}theta =csc ^{2}theta } Using these identities together with the ratio identities, it is possible to express any trigonometric function in terms of any other (up to a plus or minus sign)



Solved Cot 2 V 2 Sec V 1 Sec V 1 Tan V 2 Csc V Chegg Com



If Tantheta Cottheta 2 Find The Value Of Tan 2 Theta Cot 2 Theta
If `tan^2 thetacot^2 theta=2` then `theta=` If `tan^2 thetacot^2 theta=2` then `theta=` Books Physics NCERT DC Pandey Sunil Batra HC Verma Pradeep Errorless Chemistry NCERT P Bahadur IITJEE Previous Year Narendra Awasthi MS Chauhan Biology NCERT NCERT Exemplar NCERT Fingertips Errorless Vol1 Errorless Vol2Trigonometric identities are equations that relate different trigonometric functions and are true for any value of the variable that is there in the domainBasically, an identity is an equation that holds true for all the values of the variable(s) present in itTan 2 θ 1 = sec 2 θ;



Prove That Tan Theta Cot Theta 2 Sin2 Theta Son Theta Cos Theta 1 2 Cos2 Theta Maths Introduction To Trigonometry Meritnation Com



Rd Sharma Solutions For Class 10 Chapter 6 Trigonometric Identities Exercise 6 1 Get Pdf
Get the answers you need, now!Prove the Following Trigonometric Identities (1 Tan^2 Theta)/(1 Cot^2 Theta) = ((1 Tan Theta)/(1 Cot Theta))^2 = Tan^2 Theta CBSE CBSE (English Medium) Class 10 Question Papers 6 Textbook Solutions Important SolutionsProve that cot theta tan theta = 2 cos^2 theta 1/sin theta cos theta If playback doesn't begin shortly, try restarting your device Videos you watch may be added to the TV's watch history



Example 22 Solve Tan 2x Cot X Pi 3 Teachoo Examples


The Trigonometric Ratios Of Angl
If tan theta cot theta = 4 , then the value of tan^2 cot^2 is equal to · Tan theta cot theta = 2 then find tan²theta cot²theta = ?In various applications of trigonometry, it is useful to rewrite the trigonometric functions (such as sine and cosine) in terms of rational functions of a new variable These identities are known collectively as the tangent halfangle formulae because of the definition of These identities can be useful in calculus for converting rational functions in sine and cosine to functions of t in order



If Tan Theta Sec Theta 2 Then What Is Tan Theta Is Equal To Quora



Q69 Prove That Tan 2 8 Cot 2 8 2 Sec 2 8 Cosec 2 8 Tan Square Theta Cot Square Theta 2 Youtube
1701 · The second and third identities can be obtained by manipulating the first The identity \(1{\cot}^2 \theta={\csc}^2 \theta\) is found by rewriting the left side of the equationCot 2 θ 1 = cosec 2 Hence, to understand trigonometry further we need to learn these functions and their respective formulas at first If θ · The trigonometric double angle formulas give a relationship between the basic trigonometric functions applied to twice an angle in terms of trigonometric functions of the angle itself Tips for remembering the following formulas We can substitute the values
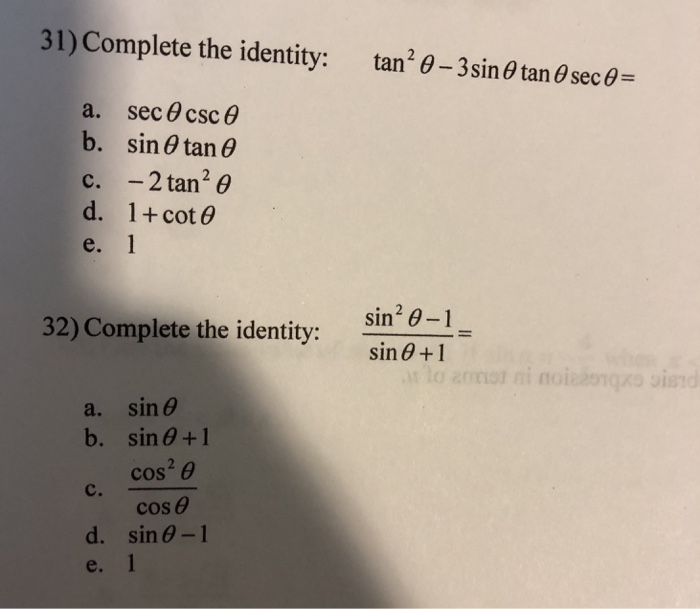


Solved 31 Complete The Identity Tan 2 8 3sin Tan 8 Sec0 Chegg Com



How Do You Verify The Identity Tan2theta 2 Cottheta Tantheta Socratic
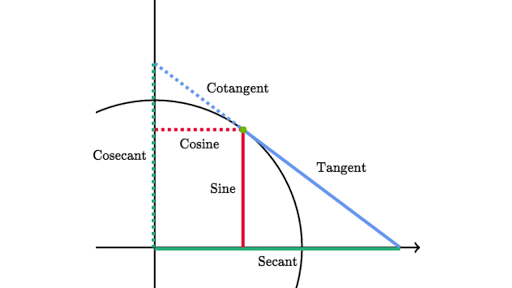
· Just apply the formula, #csc^2 theta cot^2 theta=1# so, #cot^2 theta= csc^2 theta1=7/2 1=5/2#List of triple angle identities with proofs in geometrical method and examples to learn how to use triple angle rules in trigonometric mathematics · Basic Definitions Definition of tangent $ \tan \theta = \frac{\sin \theta}{\cos\theta} $ Definition of cotangent $ \cot \theta = \frac{\cos \theta}{\sin\theta} \ $ Definition of secant $ \sec \theta = \frac{1}{\cos \theta} \ $ Definition of cosecant $ \csc \theta = \frac{1}{\sin \theta} \ $



If Tan Theta Cot Theta Is Equal To 7 Find The Value Of Tan Squared Theta Cos Squared Maths Introduction To Trigonometry Meritnation Com



Using Trigonometric Identities Video Khan Academy
· For values of tan θ use the formula tan θ = sin θ /cos θ For values the values of cot θ use cot θ = 1/tan θ For the values of sec θ use sec θ = 1/cos θ · Trigonometry Formulas Allied Angles Formula The angles 90 o θ, 180 o θ, 270 o θ and 360 o θ are knwon as allied angles The value of trigonometric ratios of these allied angles is according to the ASTC rule as discussed above Here, another rule is also used known as the odd and even multiplications of 90 o07 · To find, Value of (tan² θ cot² θ) = ?


The Trigonometric Ratios Of Angl



Prove That Cot Theta 1 Tan Theta Cot Theta 2 Sec 2 Theta Maths Some Applications Of Trigonometry Meritnation Com
2101 · Verifying Trigonometric Identities Identities enable us to simplify complicated expressions They are the basic tools of trigonometry used in solving trigonometric equations, just as factoring, finding common denominators, and using special formulas are the basic tools of solving algebraic equationsHint Use the fact $\tan^2{\theta}=\sec^2{\theta1}$ and $\cot^2{\theta} = \csc^2{\theta}1 $0812 · Trigonometric Identities (1) Conditional trigonometrical identities We have certain trigonometric identities Like sin2 θ cos2 θ = 1 and 1 tan2 θ = sec2 θ etc Such identities are identities in the sense that they hold for all value of the angles which satisfy the given condition among them and they are called



Tangent Half Angle Formula Wikipedia



14 1 Trigonometric Identities Ppt Download
Simplifying tan 2 θ cot 2 θ = 2 cos 2 θ sin 2 θ sin 2 θ cos 2 θ = 2 sin 4 θ cos 4 θ = 2 sin 2 θ cos 2 θ sin 4 θ cos 4 θ − 2 sin 2 θ cos 2 θ = 0 (sin 2 θ − cos 2 θ) 2 = 0 sin 2 θ − cos 2 θ = 0 − cos 2 θ = 0 cos 2 θ = 0 2 θ = cos − 1 0 2 θ = 2 π θ = 4 π1701 · Using graphing software, we draw the curve of y = 2 cos 2 x − sin x − 1 in the region 0 ≤ θ < 2π Wherever the curve cuts the xaxis will be the solution for our equation We see from the graph that the solutions are approximately x = 05 x = 26 x = 47 For more accurate solutions, we would just zoom in on the graph



5 1 Fundamental Trig Identities Sin 1cos 1tan 1 Csc Sec Cot Csc 1sec 1cot 1 Sin Cos Ppt Download



1 Tan 2theta 1 Cot 2theta 1 Tan Theta 1 Cot Theta 2 Tan 2 Theta Brainly In



Trigonometric Identities Topics In Trigonometry
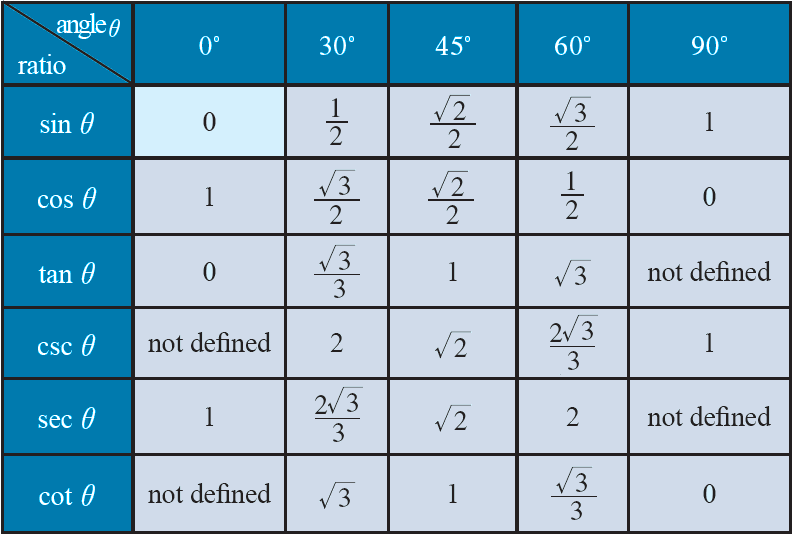


Trigonometric Formulas



Solved Establish The Identity 1 Tan 2 Theta 1 Tan 2 Chegg Com



Art Of Problem Solving
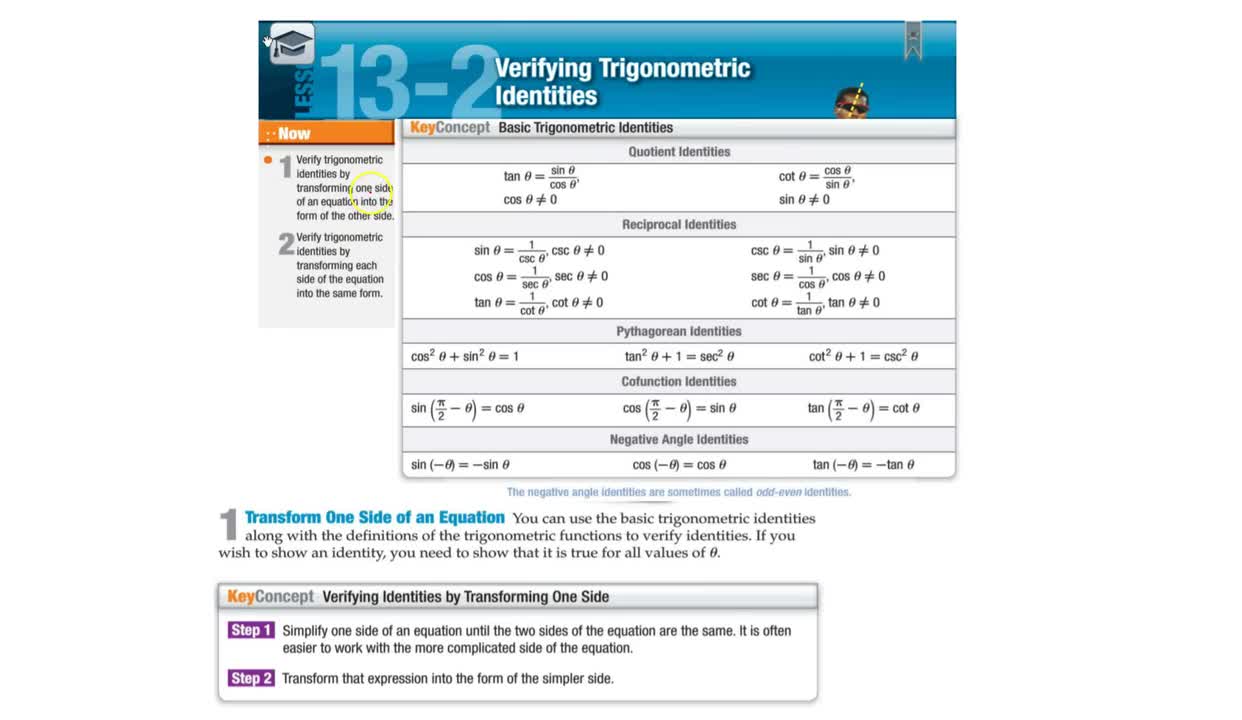


Honors Algebra 2 Trig Notes Chapter 13 Section 2 Bishop Amat Memorial High School



1 1 Tan 2 Theta 1 1 Cot 2 Theta 1 Sin 2 Theta Sin 4 Theta Brainly In


What Is The General Solution Of Tan 5 Theta Equal To Minus Cot 2 Theta Quora



1 Tan 2theta Cot Theta Cosec 2 Theta Tan Theta Brainly In
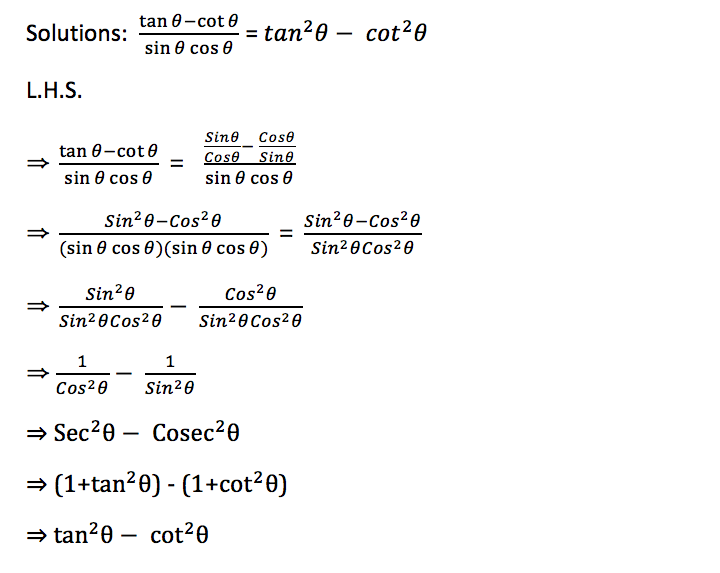


Tan Theta Cot Theta Sin Theta Cos Theta Tan 2 Theta Cot 2 Theta Class Of Achievers



Prove That Cot 8 Tan 8 2 Cos 2 8 1 Sin 8 Cos 8


Solving Trigonometric Equations With Identities Precalculus Ii
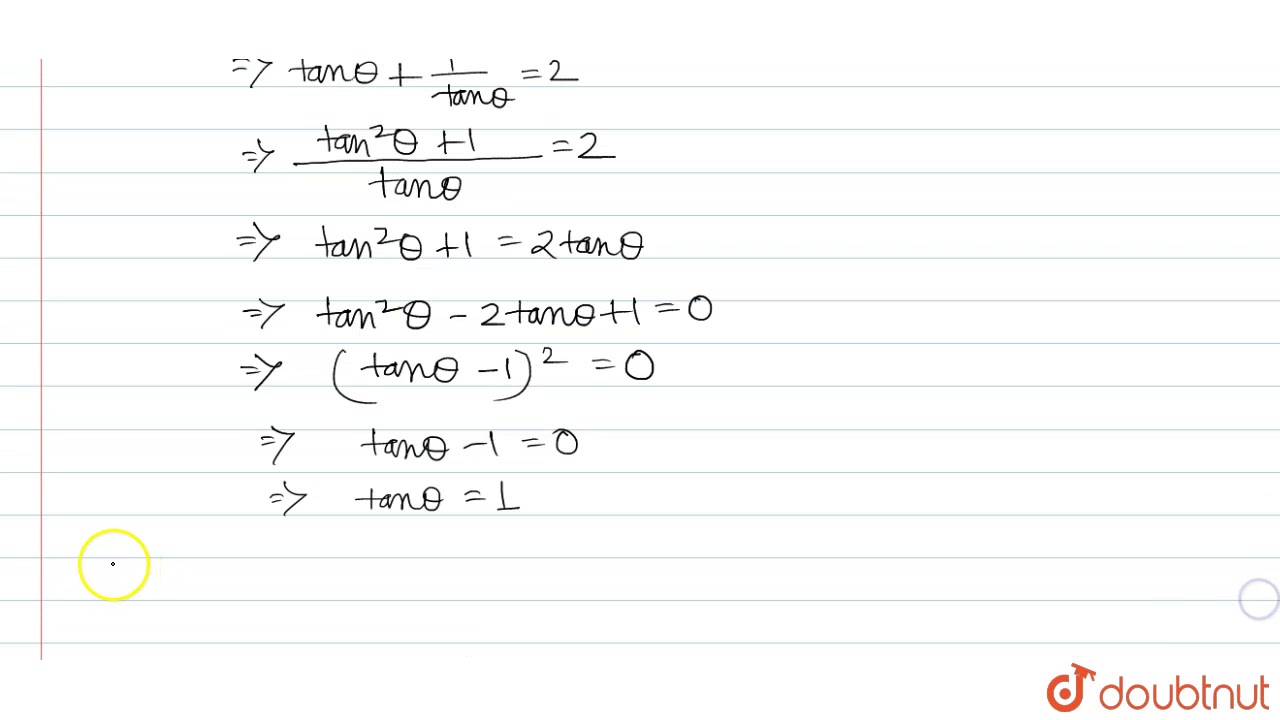


If Tan Theta Cot Theta 2 Then Dtemine The Value Of Tan Theta Cot Theta Youtube



Prove That Cot Theta Tan Theta 2 Cot 2theta Youtube



96 Prove The Identity 1 Cot Theta Csc Theta 1 Tan Theta Tan Theta Cot Theta N97 Prove The Identity Tan 2 Theta Cot 2 Theta 2 Sec 2 Theta Csc 2 Theta


How I Remember Trig Identities Part 2 Beyond Solutions



Prove That Cot Theta Tan Theta 2 Cos 2 Theta 1 Sin Theta Cos Theta Youtube



Why Is Math Csc 2 Theta Cot 2 Theta 1 Math Quora


How Do You Simplify Sin Theta Csc Theta Cot Theta Socratic


Solving Trigonometric Equations With Identities Precalculus Ii



How Does The Trigonometric Identity 1 Cot 2 Theta Csc 2 Theta Derive From The Identity Sin 2 Theta Cos 2 Theta 1 Mathematics Stack Exchange


Prove That 1 Tan 2 8 1 Cot 2 8 1 Tan 8 Cot 8 2 Tan 2 8 Sarthaks Econnect Largest Online Education Community



If Tan Theta Cot Theta 2 Then Tan 2 Theta Cot 2 Th



5 1 5 2 Trigonometric Identities Ppt Download



Trigonometric Identities List Of Trigonometric Identities Examples



96 Prove The Identity 1 Cot Theta Csc Theta 1 Tan Theta Tan Theta Cot Theta N97 Prove The Identity Tan 2 Theta Cot 2 Theta 2 Sec 2 Theta Csc 2 Theta



How Does One Prove That Math Sec 2 Theta Tan 2 Theta Csc 2 Theta Cot 2 Theta 1 2 Sec 2 Theta Csc 2 Theta Text Math Quora
x-1=sec(squared)x.jpg)


10 Identity Tan Squared X 1 Sec Squared X Trigonometry Educator Com



Prove That 1 Tan 28 1 Cot 28 1 Tan8 1 Cot8 2 Tan 28



Given Csc 2 Theta 7 2 What Is Cot 2 Theta Socratic


For All Real Values Of Theta Cot Theta 2 Cot 2theta Is Equal To Youtube


Prove If Tan 3 Theta 1 Tan 2 Theta Cot 3 Theta 1 Cot 2 Theta Sec Theta Cosec Theta 2 Sin Theta Cos Theta Edurev Class 10 Question



Solved Establish The Identity Cot 2 Theta 1 2 Sec The Chegg Com



Solved Prove The Following A 1 Sin Theta Sin Theta Chegg Com


How Do You Verify Tan 28 Sin 28 Tan 28sin 28 Socratic


How Do You Prove 1 Sin 2theta 1 Cot 2theta Cot 2theta Socratic



Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download


Trig Identity Reference Article Khan Academy



Solve The Equation Tan 2 Theta Cot 2 Theta 0 For 0 Less Than Theta Less Than 180 Degrees Study Com



Solve The Equation 2 Tan Theta Cot Theta 1 0 Youtube


Solving Trigonometric Equations With Identities Precalculus Ii



Prove Tan 2 Theta Cot 2 Theta Cosec 2 Theta Sec 2 Theta Brainly In



Rd Sharma Solutions For Class 10 Chapter 6 Trigonometric Identities Exercise 6 1 Get Pdf



If Tantheta Cottheta 2 Find The Value Of Tan 2theta Cot 2thet



If Theta Is Theta And Cos 2 Theta Cot 2 Theta Cos 2 Theta 3 Then Theta Is Equal Youtube
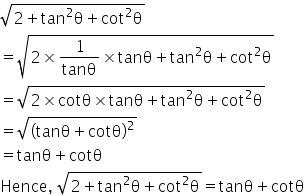


Prove That 2 Tan2 Cot2 Tan Cot Mathematics Topperlearning Com Ttevdk55



Sample Problems Cos 2 X Tan2 X Tan 2 Csc 2 Tan Sec X Tan X Cos X Sin 4 X Cos 4 X 1 2 Cos 2 X Pdf Free Download



General Solution Of Tan 5 Theta Cot 2 Theta Is Youtube



Tan Theta 1 Tan 2 Theta 2 Cot Theta 1 Cot 2 Theta 2 Sin Theta Cos Theta Brainly In


Trigonometric Identities And Equations Ppt Download



Tan 2x Cot 2x 2 Youtube



Prove That 1 Tan 2 Theta Cot 2 Theta 1 Tan 2 Theta



1 Prove That Tan2 Theta Cot2 Theta 2 Cosec2 Theta Sec2 Theta Maths Coordinate Geometry Meritnation Com



Trigonometric Identities



Prove That Tan 2 Theta Cot 2theta 2 Sec 2theta Cosec 2theta Brainly In



Prove That Cot Theta Tan Theta 2cot 2 Theta



How Does The Trigonometric Identity 1 Cot 2 Theta Csc 2 Theta Derive From The Identity Sin 2 Theta Cos 2 Theta 1 Mathematics Stack Exchange



Tangent Half Angle Formula Wikipedia



The Value Of Tan 2 Theta Cot 2 Theta Is



Prove That 1 1 Tan 2 Theta 1 1 Cot 2 Theta 1


Important Angles In Trigonometry


How To Solve The Equation 2 Tan Theta Cot Theta 1 Quora



Tangent Half Angle Formula Wikipedia



List Of Trigonometric Identities Wikipedia



Trigonometry Reciprocal Identities Expii



How Do You Verify The Identity Csctheta Cottheta Csctheta Cottheta 1 Socratic


5 1 Fundamental Trig Identities Sin 1cos 1tan 1 Csc Sec Cot Csc 1sec 1cot 1 Sin Cos Ppt Download


If Tan Theta Cot Theta 2 Then What Is The Value Of Tan Squared Theta Cot Squared Theta Equal To Quora



Solved Trigonometric Identity Equations Review Sheet Simp Chegg Com


If Cot 8 Tan 8 2 Cosec 8 Then Find The General Value Of 8 Studyrankersonline



Rd Sharma Solutions For Class 10 Chapter 6 Trigonometric Identities Exercise 6 1 Get Pdf



Solved Csc Theta Cdot Cos Theta Cot Theta Sec Theta Chegg Com



Worksheet On Trigonometric Identities Establishing Identities Hints



Prove 1 Cot 2 Theta Csc 2 Theta Mathematics Stack Exchange



If Tan Theta Cot Theta 2 Then What Is The Value Of Tan Squared Theta Cot Squared Theta Equal To Quora



No comments:
Post a Comment